Формализация логического закона достаточного основания

30 мая 2020 года во время диалектического обсуждения методологии статьи в разделе Александра Леонидовича Бурылова (Пермского) (Кормин Михаил, 30 Май, 2020 - 20:51, ссылка) совершенно случайно мне пришло в голову как формализовать правило достаточного основания логики высказываний. Правило впервые было сформулировано Лейбницем.
«…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, — без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны»
— Лейбниц, «Монадология»
Правило достаточного основания, несмотря на то, что стоит в одном ряду с таким основополагающими законами логики, как закон тождества, закон исключенного третьего, закон запрещенного противоречия до сих пор не формализовано. Оно дополняет основную триаду логических законов, опираясь только на основания здравого смысла. Формализация в состоянии превратить этот, безусловно полезный принцип теоретического мышления, в полноценный логический закон. Вопросов как назвать новый формализованный закон логики у меня не возникло. Как автор формализации, я называю его «Формализованный Закон Достаточного Основания Лейбница». Формализация опирается на общепринятый символьный аппарат формальной логики и таблицы истинности. Никаких изменений в существующий матаппарат не вносится.
Формализация правила достаточного основания.
Начнем с единственной аксиомы на которую будет опираться Формализованный Закон Достаточного Основания Лейбница.
Импликация истинна тогда и только тогда, когда посылка включена в следствие.
В качестве доказательства аксиомы возьмем таблицу истинности импликации. В соответствии с общепринятыми стандартами математической логики когда истинно принимается 1, а лож принимается 0, можно использовать графическое представление полного соответствия таблицы истинности импликации аксиоме.

Во всех трех случаях когда импликация истинна, посылка включена в следствие. В единственном случае когда импликация ложна следствие включено в посылку.
Графическое представления я буду использовать и дальше, для того, чтобы показать в чем коренное различие Логического Квадрата Аристотеля, от логики эквивалентности, на которую опирается закон достаточного основания Лейбница.

Логический квадрат Аристотеля учитывает все возможные варианты Логики предикатов первого уровня. Множество субъектов S может как обладать свойством P, так и не обладать им. В том числе учитывается, что часть субъектов S может обладать свойством, а другая часть им не обладать. Недостаток логического квадрата в том, что все множество свойств, которые после последовательных итераций можно выявить у постоянно уменьшающегося множества субъектов оказываются предикатами первого уровня.
Вложение свойств друг в друга (категории) не предусмотрено логическим квадратом Аристотеля, поскольку отрицание множества субъектов нарушает фундаментальный закон логики «Закон Тождества». Для вложения свойств друг в друга в мат аппарате формальной логики используется логика предикатов высших порядков.
Графическое изображения квадрата вложения свойств друг в друга отличается от Логического квадрата Аристотеля поскольку запрет на отрицание субъекта снимается переходом на второй уровень вложения свойств. Само множество субъектов обозначаемое в символьных записях (s) не отрицается, и соответственно закон тождества не нарушен. А вот свойства могут отрицаться в независимости от уровня вложения, без разницы первого или второго.
Я называю этот квадрат логикой эквивалентности поскольку в сумма контрарных отношений квадрата составляет запись эквивалентности свойств. Но по сути, этот квадрат можно смело назвать логическим квадратом Платона, поскольку он полностью соответствует тому, что утверждал Платон под наукой «Философия».
"Моя теория содержит "идеи", или "форм". Эта теория является частично логической, и частично метафизической. Логическая часть имеет дело со значением общих слов. Когда ряд индивидов имеет общее название, они имеют также общую "идею" или "форму". Например, имеется много отдельных животных, о которых мы можем точно сказать: "Это кошка", но существует лишь одна "идея", или "форма", кошки. Что мы подразумеваем под словом "кошка"? Очевидно, нечто отличное от каждой отдельной кошки. По-видимому, какое-либо животное является кошкой потому, что оно разделяет общую природу, свойственную всем кошкам. Язык не может обойтись без таких общих слов, как "кошка", и такие слова, очевидно, не являются бессмысленными. Но если слово "кошка" означает что-либо, то оно означает что-то, не являющееся той или этой кошкой, а представляющее собой нечто в роде универсальной кошачности. Она не родилась, когда родилась отдельная кошка, и не умрет вместе со смертью отдельной кошки. На самом деле она не имеет места в пространстве или времени: она "вечна". Это логическая часть теории. Аргументы в ее пользу, независимо от того, являются они, в конце концов, безусловно верными или нет, сильны и совершенно независимы от метафизической части этой теории. Согласно метафизической части этой теории, слово "кошка" означает некоторую идеальную кошку. Об этой одной "кошке", созданной Богом, и единственную в своем роде, возможно знание. Отдельные кошки разделяют природу Кошки, но более или менее несовершенно, являясь лишь копиями "идеи". Только благодаря этому несовершенству может быть много кошек. Идеальная Кошка реальна: отдельные кошки являются лишь кажущимися, и в отношении многих кошек, сделанных Богом, может быть лишь мнение. Я признав идею первопричиной всего сущего, определяю и основную задачу философии, и предмет науки как познание мира идей, которое возможно лишь посредством диалектического процесса мышления как процесса образования и разделения понятий, и выявление их совместимости (или несовместимости) с предметным миром." Платон
Платон отделяет чтойность Р от множества субъектов (s) и тем самым снимает запрет на отрицание субъекта наложенный фундаментальным законом Тождества. Это дает возможность итерационно плести из предикатов первого уровня семантические цепи какого угодно уровня вложений. Пирамида категорий может быть бесконечной, но для отдельной итерации всегда используется один и тот же логический квадрат.
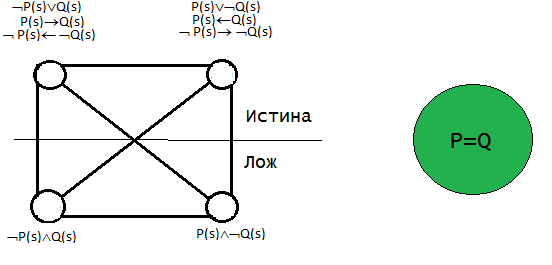
Логический квадрат Платона имеет четыре агрегатных состояния в соответствии с двумя горизонтальными и двумя вертикальными делениями.
1) Эквивалентность свойств.
2) Не связанность свойств.
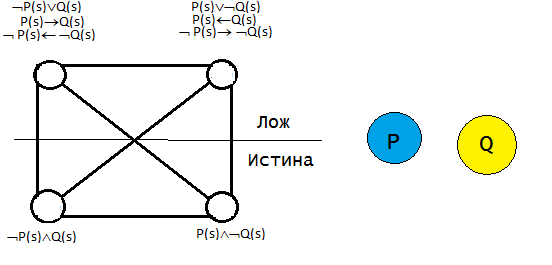
3) Видовой признак.
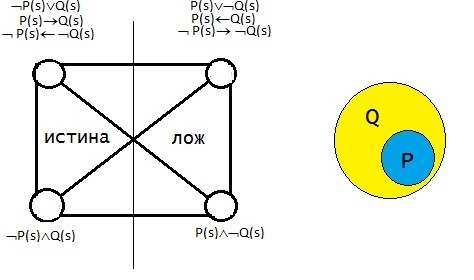
4) Родовой признак.
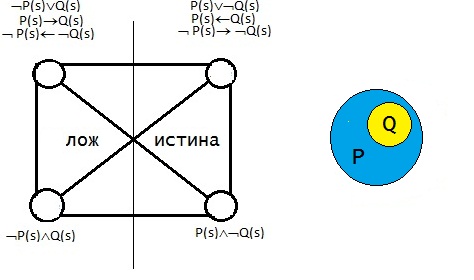
Контрадикторные отношения в логическом квадрате Платона, в точности так же как и в логическом квадрате Аристотеля предполагают смену квантора. Взаиморасположение логического квадрата Аристотеля и логического квадрата Платона можно показать на графическом изображении логической звезды.

В качестве контрарных отношений квадрата эквивалентности (красный квадрат) выступают импликация и репликация. И в том и в другом случае под квантором общности нет необходимости привлекать логическую операцию отрицания.
В случае, если будет заранее известно, что понятия, скрывающиеся под переменными связаны родовым, либо видовым признаком, то достаточно выявить истинное высказывание под квантором общности, чтобы его пара в контрарных отношениях без вариантов оказалась ложной.
Отсечь состояния №1 и №2. горизонтального деления логического квадрата Платона на истинную и ложную часть нам поможет аксиома подтвержденная таблицей истинности импликации.
Импликация истинна тогда и только тогда, когда посылка включена в следствие.
Аксиома в трех из четырех случаев подтверждает что посылка и следствие связанны и неэквивалентны. Единственным пограничным случаем, когда ложная посылка вложена (либо эквивалентна) в ложное следствие можно пренебречь из соображения здравого смысла.
Поскольку формальные записи мат аппарата логики высказываний практически не отличаются от мат аппарата логики предикатов за исключением обязательного отображения кванторов, и обозначения переменных не строчными а прописными буквами, будем считать, что само наличие операции импликации либо репликации уже считается введением квантора общности.
В случае, когда аксиома, отсекает горизонтальное деление квадрата эквивалентности остается только вертикальное деление. Истинность правой части квадрата, означает ложность левой части квадрата и наоборот. Это аналог контрадикторного противоречия, но уже записи контрарных отношений несовместимы ни по лжи, ни по истине, без перемены квантора. Это дает возможность отобразить формализованный закон достаточного основания Лейбница в форме закона исключенного третьего и запрещенного противоречия.
(S -> P) v (S <- P) = 1
(S -> P) ˄ (S <- P) = 0
С чисто формальной точки зрения, формализованный закон достаточного основания Лейбница – аналог трехзначной математической логики (истинно, лож, не определено). Но вместо значения «не определено», используется значение «не рассматривается», поскольку, не рассматриваемые варианты не неопределены, а отсечены аксиомой.
Сравнительный анализ раскрытия законов исключенного третьего и непротиворечия через логический квадрат Аристотеля, и формализованный закон достаточного основания Лейбница представлены в следующей презентации.

Формализованный закон достаточного основания Лейбница, в отличии от логического квадрата Аристотеля, позволяет работать с абстрактными конструкциями любой степени вложения. Это не означает, что привязка к квантору существования не нужна. Это означает, что теория может в любой момент спустится с любого горизонта абстракции и свериться с фактами чувственного восприятия. Квадрат логики эквивалентности располагает такой возможностью, она просто не рассматривается без насущной необходимости.
Образным языком, это корабль снабженный компасом, который следует заданному направлению в открытом море, в отличии от корабля без компаса, который вынужден идти вдоль берега сверяя курс по береговой линии.
Применимость Формализованного Закона Достаточного Основания
Формализованный закон достаточного основания Лейбница однозначно выявляет обоснованность, истинность и ложность речевых оборотов: потому что, следовательно, если….то, и других аналогов использования операций импликации и репликации в рассуждениях, тремя способами.
Истинно
Ложно
Не обоснованно
Обоснование применения логической операции репликации, одновременно является обоснованием логической операции импликации и наоборот.
Не имеет значения разговорная это речь здесь и сейчас, или текст любой давности.
Практическое применение формализованного закона достаточного основания Лейбница.
Если взять два высказывания не различая изначально которое из них посылка, а которое следствие то истинное следствие согласно аксиоме «Импликация истинна тогда и только тогда, когда посылка включена в следствие» можно вычислить по вложению в него посылки.
Например "ветер дует" "деревья качаются"
Если не только ветер, но и я могу покачать дерево. Значит "деревья качаются" следствие. В "деревья качаются" кроме ветра включены и другие сторонние силы способные их покачать.
В соответствии с формализованным законом достаточного основания мы вправе утверждать.
Деревья качаются, потому что ветер дует (истинно)
Ветер дует, потому что деревья качаются (ложно)
Применение речевого оборота «потому, что» обоснованно.
В качестве практики применения разберем примеры приведенные в википедии к неформализованному правилу достаточного основания.
1)Это вещество является электропроводным, потому что оно — металл.
Это по сути логика предикатов, поскольку посылка и следствие представлены понятиями, но не высказываниями.
Хорошим проводником электричества кроме металлов является вода. Не только металл, но и вода проводит электричество. Электропроводность – следствие. Металл - посылка.
Электропроводен, потому что металл – истинно.
Металл, потому что электропроводен – ложно.
Применение речевого оборота «потому что» обоснованно.
В данном примере использована логическая операция репликации. В случае если использовать логическую операцию импликации суждение будет выглядеть следующим образом.
Если металл, то электропроводен – истинно
Если электропроводен, то металл – ложно.
Металл, следовательно электропроводен – истинно
Электропроводен, следовательно металл – ложно
Поскольку формализованный закон достаточного основания Лейбница аналог трехзначной логики я не могу сказать однозначно ДРУГИХ ВАРИАНТОВ НЕТ.
Если эта причинно-следственная связь является узловым элементом теории необходимо свериться с фактами. Нашли научные сотрудники неэлектропроводные металлы, или нет. Если нашли, то понятия электропроводность, и металл более не рассматриваются в рамках формализованного закона достаточного основания Лейбница. Это уже не связанные понятия, которые отсекаются аксиомой. Соответственно применение речевых оборотов заменяющих операции импликации и репликации становится необоснованным.
2) «Не ставьте мне двойку, спросите ещё, я же прочитал весь учебник (основание), что-нибудь уж точно отвечу (тезис)»
Этот пример нужно привести в форму импликации, либо репликации. По смыслу больше подходит репликация.
«Не ставьте мне двойку, спросите ещё, что-нибудь уж точно отвечу, потому что я прочитал весь учебник».
Посылка и следствие не вкладываются друг в друга. Это несвязанные высказывания. Можно прочитать весь учебник, но ничего не ответить, а можно что-нибудь ответить, не читая учебник. Связки высказываний посредством импликации и либо репликации не обоснованы.
Применение речевого оборота «потому что» не обоснованно.
«Преступление совершил Н. (тезис), ведь он сам признался в этом и подписал все показания (основание)»
Приводим в форму репликации.
«Преступление совершил Н. , потому что он сам признался в этом и подписал все показания»
Пример аналогичен предыдущему. Можно совершить преступление, но не сознаться в этом, а можно не совершать преступление, но сознаться. Высказывания не связанны между собой. Применение операции импликации, либо репликации необоснованно.
Применение речевого оборота «потому что» не обоснованно.
То, что мне приходится приводить примеры из википедии к формальной базе нисколько не говорит о ущербности формализованного закона достаточного основания Лейбница, просто эти примеры искусственны. Связка импликации и репликации, основные связки мыслительного аппарата любого человека. По поводу каждого случая применения такой связки в опубликованном тексте можно вынести однозначный формальный вердикт. Обоснована она, или не обоснована, истинна или ложна.
Каждый раз, когда причинно-следственная связь, укоренившаяся в мировоззрении теряет свой статус истинности человеку немножечко больно. Неважно, обретает эта связь статус ложной, или необоснованной. Думайте об этом, когда применяете этот закон на практике.
Данная публикация не требует одобрения ни одного ученого совета любой Академии наук, поскольку в доказательствах применяются символьные записи и таблицы истинности, действенные во всех возможных мирах. Я выбрал ФШ в качестве резервации авторского права на формализацию «Формализованного закона достаточного основания Лейбница» только потому, что он был открыт именно на этой площадке. ФШ специализированный ресурс, который открывался для обсуждения актуальных философских вопросов, а не как ресурс для людей, которым не с кем поговорить. От комментариев с критикой самой формализации я жду сопровождения символьными записями, либо графическими материалами.
Вот таких результатов можно достичь, если не доказывать свою правоту с пеной у рта, а помогать другу развивать собственное мировоззрение посредством диалектической дискуссии.
- Кормин Михаил
- Для комментирования войдите или зарегистрируйтесь

Комментарии
Импликация (от лат. implicatio — «связь») — бинарная логическая связка, по своему применению приближенная к союзам «если…, то…». Импликация записывается как посылка. следствие; ...
Чем импликация отличается от посылки?
Основание будет достаточно тогда, когда посылка оставляет свой след. След именно этой посылки, а не другой.
Владимир. В Символьной логике следов быть не может. Эта самореферентная теория не реагирует на количество. Там есть только двоичный код (1:0)
Например.
Если включить выключатель, то загорится лампочка.
Лампочка может как гореть, так и не гореть. С включенным выключателем лампочка горит. Посылка включена в следствие. Не исправности электоропроводки, мы не рассматриваем, то, что она исправна задано условиями задачи.
Откуда тогда взялась "посылка"?
Что за "посылка"? Пошлите вместо электрического тока, ток воды, - лампочка загорится?
Импликация истинна тогда и только тогда, когда посылка включена в следствие - это не я придумал.
Но полностью понимаю "включение посылки в следствие".
Откуда мне знать. Это у историков философии спросить надо, кто этот термин ввел. Искусственный язык. За каждым термином стоит причина со своими инициалами. Не обязательно это ФИО, но что нибудь подобное.
Мне зачем вводить новые термины. Ту часть символьной записи, которая смотрит на стрелочку сзади обычно называют либо антецедентом (Кантовская школа), либо посылкой (? кто придумал). А ту часть которая смотрит на стрелочку спереди обычно называют консеквентом (Кантовская школа), либо следствием (? кто ввел)
А вот у Воды нет достаточного основания включить лампочку, поскольку посылка не включена в следствие. И у угля нет достаточного основания. И у акумулятора. Это проблема электросети. А она исправна по условиям задачи.
В переводе на русский: вода (посылка) не может залезть в лампочку, поэтому лампочка и не горит (следствие). А вот если бы вода смогла залезть в нить накаливания, то, кто знает, может лампочка бы и загорелась.
В вашем примере неверна сама методология.
Пример Кормина с электричеством и лампочкой лишь пример мысленного процесса.
Вы заменили электричество на воду, но оставили лампочку. Получилось: в огороде бузина, а в Киеве дядька.
При замене электричества на воду, для сохранения аналогии нужно и лампочку заменить на крыльчатку.
Получаем две равнозначные аналогии: при включении тока электронов лампочка светит.
При включении тока воды, крыльчатка вращается.
Ваша "вода в лампочке" это не аналогия, а формулировка гипотезы, требующей опытной проверки. В этом смысле я согласен с вами: При определенных условиях для освещения можно использовать и воду (нужно только найти эти условия).
Эти мои суждения пример практического использования законов необходимого и достаточного основания.
Это и есть закон достаточного основания; если "послали воду", то и "получить" надо воду, а не "электричество" или "свет". А потом из движения воды надо выделить достаточное основание, чтобы можно было говорить о "движении электричества".
Михаил, пока один формальный вопрос.
В старттопике приведен большой текст в кавычках за подписью Платон:
Очень сомнительно, что это цитата из Платона. Это что и как понимать?
Это из переписки с Аристотелем. Там вся переписка просто бомба. Точную ссылку сейчас искать некогда. И Аристотелевские и Платоновские тексты эталон логики мышления.
Тоже чето не могу найти. Дело было так. Когда мы проходили древний мир. Нам выдавали список литературы обязательный для прочтения. Чтоб читали оригинальные тексты, в устраивающем препода переводе, а не комментарии современников. Препод был Плотиник, по специализации. На древнегреческом соображал не хуже чем на русском. Если бы ему статус позволял, то он бы нас еще и на оргинальном языке читать заставил. Короче не читать было нельзя.
А я просто копипастил цитаты которые мне понравились. Сейчас беру из своих запасников.
Ну тогда дело вообще швах, потому что уж очень большая вероятность подмены, фальсификации. Мои контрагрументы.
Аристотель действительно называл идеи формами, но вряд ли Платон.
Ни тот, ни другой не знали слова "метафизика". Оно появилось позже.
Пример кошки очень не по духу античности, скорее, был бы пример с горшком, конем или человеком.
Идею кошки вряд ли Платон считал отличной от самой кошки, скорее, он считал их подобными, состоящими в отношении образца.
Ни в коем случае Платон не увязывал бы идею кошки, как у Вас в тексте, со словом "кошка". Идеи у него существуют в ином (идеальном) мире, чем слова.
Универсальная кощачьесть - это, точно, платоновско-аристотелевская мысль.
Платон, конечно, знал о теории (феории), но вряд ли мог употребить такие современные слова, как "логическая часть теории".
О создании идей Богом - это вообще из серии каких-то христианско-теологических спекуляций. А то, что отдельные кошки являются лишь кажущимися - это из серии древнеиндийской майи.
"Диалектический процесс мышления как процесс образования и разделения понятий" - совсем не платоновский язык, а скорее марксистско-ленинский.
Я думаю дело не в фальсификации, а в влиянии идеологии духа времени на переводчика. Перевод древних текстов, это как раз адаптация, делающая эти тексты доступными для понимания современников.
Значит речь скорее всего о переводчиках советского периода. Эта проблема поставлена уже в 90х годах.
Это из введения к изданию
А. Ф. Лосев
А. А. Тахо-Годи
ПЛАТОН • АРИСТОТЕЛЬ
Серия "Жизнь замечательных людей" впуск 1147 (947)
Ссылку давать не буду, там реклам видимо не видимо. Если интересно, то лучше бумажную версию книжки в библиотеке взять.
Основной вопрос который меня сейчас занимает, откуда взялся в рефератах студенческих этот не существовавший диалог.
Не сами же студенты его придумали. Им такой полет фантазий не по зубам. Скопипастили откуда-то. Откуда растут ноги аргументации Аристотеля я выяснил. Это замечательная книжка Лосева А.Ф.
Её тоже лучше взять в библиотеке. Столько рекламы в сети, что всякое желание читать пропадает. А книжка очень хорошая. Там как раз спор о числах. Если логику древних изучать, то в самый раз.
Сейчас осталось найти, откуда растут ноги аргументации Платона. И я бы очень хотел, чтобы это тоже была какая-нибудь из работ Лосева. Найти более добросовестного историка философии, невероятно сложно. Там обязательно будут ссылки на древние тексты на оригинальном языке.
Будем искать.
Михаил, боюсь у нас с Вами разные переводческие культуры.
Для серьезных исследований я предпочитаю всегда читать только первоисточники. По возможности сверяясь с языком оригинала (во всяком случае в центральных терминах). В свое время даже сам сделал перевод фрагментов Анаксагора (могу выслать книжку). Мои микроопыты по фразе Гераклита можете посмотреть в параллельной теме - ссылка.
Поэтому я не стал бы тратить столько время на студенческие эксперименты и придавать им такое значение. Хотя по беглому прочтению вижу, что Аристотель передан там более менее адекватно (наверное, потому, что от Лосева), а Платон вообще не в жилу ("создан" просто по принципу "от обратного"). Поэтому и удивился интерпретации Платона в Вашем тексте.
Хотя есть более аутентичная критика идей Платона самим Аристотелем в его "Метафизике".
Я вообще не увлекаюсь историей философии. Для этого нужно владеть оригинальным языком. Как первооткрватель логического квадрата, я имею право назвать его любым именем. Хоть именем любимой жены, хоть именем любимой собаки.
Я выбрал Платона. Основа выбора предоставленный текст. Именно этот текст натолкнул меня на размышления, в эту сторону. Даже если это сфальсифицированный Платон, этого для меня достаточно, чтоб остановиться на этом имени. Если историки философии будут сильно против моего выбора, то я, как автор, просто пошлю их нафиг. И буду сто процентов прав.
Синенький логический квадрат имеет устоявшееся историческое название. "Логический квадрат Аристотеля". Хотя сам Аристотель к нему возможно тоже не имеет никакого отношения. По крайней мере, в той же метафизике, я никаких квадратов не видел.
Книжка Лосева
Как раз перевод 13 и 14 книг метафизики Лосевым. Доверять Вам больше чем Лосеву у меня оснований пока нет.
Найду ссылку на оригинальный текст. Обсудим нюансы перевода.
Я всегда занимаюсь только тем, что мне интересно. Слово надо, для меня, не существует. А вот мое, не хочу, не обсуждается. Я же говорю, самодур, деспот, тиран.
Я буду искать.
Михаил, я же с Вами согласился. Ваша логическая концепция является оригинальной и имеет самостоятельное теоретическое значение. Она не нуждается ни в каких внешних притягиваниях за уши имен Парменида, Платона, Аристотеля (последнего разве что исключительно номинально - для обозначения "квадрата", но не сути его мышления, понимания ума и метафизики). Я бы сосредоточился на более подробной экспликации Вашей модели "круга-шестиугольника" со встроенными в него прямоугольниками. Это многим непонятно. Тогда и более наглядным станут доказательства многих законов логики. Это очень интересно. И эвристично.
Хорошо. У меня уже есть запрос довести систему с 10, до 16 булевых функций. Доведу в ближайшее время.
Загляните в личные сообщения.
Со статье ознакомился. Понял цель и парадигму. Механизм доказательства понятен и доступен даже для неподготовленного читателя, но... для использования его как инструмента необходимо тщательное изучение и постоянная практика методики применения.
В неформальном виде, из опыта решения практических задач, я использую закон достаточного основания ещё со школьных времен: Это количество знаний необходимо и достаточно для решения данной задачи.
Это методологическое объединение двух законов - закона необходимого основания и закона достаточного основания.
Закон необходимого - это обязательное определения необходимых знаний и средств для решения поставленной задачи. В противном случае задача будет не решена (проблема не устранима).
Закон достаточного - это Бритва Оккамы - нет необходимости в привлечении лишнего...
Пример: Для нахождения двух неизвестных необходимо знать правила составления системы уравнений и нахождения неизвестных. Это нижняя граница знаний, необходимых для решения этой задачи.
Для... достаточно знать правила составления системы уравнений и нахождения неизвестных и иметь опыт использования этих знаний. В знаниях законов тригонометрии, физики и прочего нет необходимости.
Это правило действует и в нашем случае. парадигму я понял, а вот в полном знании этого метода у меня нет необходимости, за что и прошу прощения.
Согласен. Поскольку речь идет о философской методологии (а не, скажем, об информатике или сопромате), то я и попросил Михаила увязать логические алгоритмы с практикой философствования хотя бы самых великих классиков, чтобы потом на их опыте можно было применять уже повсеместно.
Первое, поверхностное впечатление: "Видите трещины штукатурки на потолке? Это и есть таблица истинности..."
А в общем впечатляет, надо ещё раз прочитать от начала и до конца, возможно дойдёт...
Михаил, куда Вы пропали?
Я за это время окончательно определился с формулой ЗДО - см. ссылка.
И выразил Вам благодарность за сотворчество.
Хотелось бы знать Ваше мнение по формуле.
То есть, комментариев вы ждёте только от тех, кто уже согласен вами, что закон достаточного основания поддаётся формализации. Поскольку
То есть, достаточным основанием для суждения "Закон достаточного основания формализуем" для вас является "применение символьных записей и таблиц истинности, действенные во всех возможных мирах". Но это смех, а не достаточное основание.
В самом деле, "символьные записи и таблицы истинности" могут признаваться истинными только тогда, когда они, по отдельности, имеют достаточное основание. Поэтому сами по себе "символьные записи и таблицы истинности" не могут являться достаточным основанием для суждения "Закон достаточного основания формализуем".
В любом случае - мы с Михаилом хотя бы попытались поискать такое решение и предложили формулу. Доп. см. ссылка.
А что от Вас? Одни злорадствующие реплики. Вот это точно смех: участвовать в дискуссии, чтобы попинать оппонента. Предложите свое решение проблемы достаточного основания. Тогда посмотрим, в каком месте смеяться. Ждем-с...
Никакой проблемы нет, поскольку закон достаточного основания не формализуем.
Закон достаточного основания формулируется так:
А достаточным основанием может быть разное. Например:
Какая может быть формализация этого разного? Никакая.
Формами мышления являются: понятие, суждение, умозаключение... Понятие вне характеристики истинно или ложно. А начиная с суждения такая характеристика правомерна. Поэтому закон достаточного основания применим в основном к суждениям. Суждения должны иметь достаточные основания, а потому признаваться истинными. А дальше уже логические операции с суждениями.
Приведите хотя бы один закон, подтвержденный практикой, который не имеет вариационного результата. Любое подтверждение практикой законность основывает на релевантных статистиках. Это приближение к 100% с более менее удовлетворительным результатом.
Это вашими конкретно формами мышления являются: понятие, суждение, умозаключение. У меня этот набор шире. Там есть еще вопросы, оценки, императивы.
Это оценка. Формой мышления она, по вашему, не является. Какого понимания Вы тогда ищете. Вначале приведите свое сообщение в рамки форм мышления.
Ну и я не принуждаю Вас уверовать в формализацию закона достаточного основания.
Википедия в помощь.
https://ru.wikipedia.org/wiki/Закон_достаточного_основания
Тем более если я начну пропускать ваши конкретно сообщения через формализованный закон достаточного основания.
То эти сообщения совсем не совпадут с вашими же картинками.
Вы с завидной регулярностью подтасовываете под отношение подчинения (3) либо отношение несовместимости (4) либо отношение пересечения (2).
Примеров этих подтасовок в ваших текстах масса. Если хотите, я их здесь внимательно и скурпулезно разберу. Хотя сама картинка мне понравилась. Очень напоминает мою. Только моя систематизирована относительно кванторов.
Очевидно, в логике учёного это учитывается применительно к решаемым вопросам. Но вы-то здесь излагаете не логику учёного, а просто логику.
У меня после слова "умозаключение" многоточие. Вы знакомы с таким символом?
Почему не является? Это суждение. Можно без потери смысла написать: "Это не достаточное основание". Общеотрицательное суждение.
Собственно, это не мои картинки. Это пояснение кругами Эйлера приводится в книге Дмитрия Гусева "Краткий курс логики: Искусство правильного мышления". (ссылка, стр.7) Я разделяю, потому воспроизвёл.
Дмитрий Алексеевич Гусев (15 мая 1969) — доктор философских наук, профессор кафедры философии Московского Педагогического Государственного Университета им. В.И. Ленина (ссылка).
Всё правильно:
А вы можете дальше формализовать закон достаточного основания. Если хотите.
Доказательства, что ЗДО не формализуем, не приведено. Есть просто высказывания ряда авторов, и Вас в том числе, что им так видится. Ну видится и видится. Для теоремы Ферма тоже несколько сотен лет не видели, а потом кто-то взял и доказал. А здесь и доказательство приведено. Хотя бы грамотно научно тогда его фальсифицируйте, а не просто мнение высказывайте.
Я в двух сообщениях обосновал, что суждение "Закон достаточного основания формализуем" достаточного основания не имеет. Следовательно, либо это суждение ложно, либо достаточное основание еще нужно поискать. Ищите, кто вам не даёт?
А пока утверждение, излагаемое в Википедии, в силе:
Ну Википедия нашей формулы ЗДО не видела, с нее спроса нет. А Вы видели, и уже прогресс, что разрешили:
Спасибо. Продолжаем искать. Хотя понятно, что оно в нашей формуле сокрыто.
Если это суждение рассмотреть в качестве импликации: «Импликация истинна тогда и только тогда, когда посылка включена в следствие» ! Не соображу, что здесь может служить в качестве посылки!?
А я не понимаю, зачем вы захотели рассмотреть это суждение в качестве импликации? Я о нём утверждаю только то, что оно не имеет достаточного основания, а потому не может быть признано истинным.
Вот из книги И. Демидова "Логика: Учебное пособие для юридических вузов", я это имел в виду:
Не знаю, может дело в другом? Михаил предлагает ЗДО считать "формализованным", если основание (посылка) удовлетворяет условию аксиомы: "Импликация истинна тогда и только тогда, когда посылка включена в следствие" !
Изврат позиции: он не просто предлагает считать, он предлагает формулу ЗДО:
Я тоже предложил аналогичную формулу:
Вы обе формулы проигнорировали и снова извратили.
Импликация не есть формула ЗДО. Формула ЗДО - дизъюнкия импликации и репликации. Читайте внимательно.
Да, вот теперь, кажется, я начинаю понимать Владимира К. Вы, Сергей, с Михаилом ребята хотя и напористые, но безответственные, по-видимому!? Принцип достаточного основания широко используется и успешно применяется в науке. И в большей своей части принцип достаточного основания служит для верификации или подтверждения теоретических взглядов опытным фактам! Вы же предлагаете, принцип ДО подчинить сугубо бумажной "волоките", формализовав его для "практики" своего ума! Потому-то, в силу практической значимости, этот принцип ДО и не может быть принят в качестве закона формальной логики! ...и нечего страдать, если ещё помните что изучает Логика!?
Это неверно. А если шире взглянуть на то, что он предлагает, так это онтологические и когнитивные основания логики свести к одним только когнитивным основаниям.
То есть, нынешнюю логику, подобную физике, низвести до логики, подобной алхимии.
Скорее, сфера онтологии, в которой зачастую и применим принцип достаточного основания, лишь малой толикой касается оснований логики. Логика наука о мышлении, а не о мире в целом! Поэтому и нельзя
Интересно, что Вы называете онтологическими основаниями в Логике?
Ну, считать Логику подобной Физике - это верх "нахальства", хотя говорить о физических свойствах мышления так же возможно и нужно!
Я вот что имел в виду.
Если говорится -
- то замах Кормина и Борчикова такой, чтобы "содержание данного основания" не определялось "содержанием соответствующей отрасли знания", а просто вытекало из "содержания соответствующей отрасли знания", формальным образом. Но тогда у логики уже не будет никаких онтологических оснований.
Относительно самих онтологических оснований логики я мало размышлял, поэтому ничего стоящего на данный момент сказать не могу.
Обоим Владимирам
Примитивизм детского сада. Ежу понятно, что все а, в, с, d, х, у, S, P, стрелки, причины, основания, посылки, следствия и т.д. открываются, и берутся, и верифицируются в соответствующих отраслях знания. Тем не мене при этом формируются логические структуры, которые могут быть описаны законами логики. Остальное вытекает из сказанного.
Этим вы только подтверждаете мою мысль о вашем, с Корминым, замахе.
Человек мыслит одновременно в разных ипостасях, как специалист внутри какой-нибудь науки, как учёный этой науки, как просто учёный и как просто человек. Последнее является предельным обобщением качества мышления. А согласно вашему утверждению, предельным обобщением у вас является "как просто учёный". Предельное обобщение "как просто человек" исключается. Но вместе с этим исключением исключаются и онтологические основы логики.
В книге по логике написано "Это определяется содержанием соответствующей отрасли знания". А у вас "...открываются, и берутся, и верифицируются в соответствующих отраслях знания".
Нет, Сергей, не видно что вам понятно. С одной стороны вы соглашаетесь, что принцип достаточного основания находит своё воплощение вне логических прикладных областях науки, а с другой стороны заявляете, что это закон о формах мышления! В таком случае, вам ничего не остаётся как показать, что бытие есть то и только то, которое в мышлении (помните как у Парменида - мышление тождественно бытию)! Сможете это показать, не пускаясь в пустые декларации?
Да, мне тоже сдаётся, что универсальный принцип познания природы "затаскивать" в рамки Логики - это форменная авантюра!
У меня наоборот. У них потуги логику туда затащить, лишить её самодостаточности.
По любому, им проставляться! Ящик минералки - не меньше, если не докажут тождество Бытия и Мышления!
Здесь на форуме никто не сдаётся, а ломит свою позицию до гроба.
Что и гробы будут исписаны "закорючками" ?
?
Впервой что ли? Даже Пушкин на "берег дальный" самую малость рассчитывал:
Что в имени тебе моем?
Оно умрет, как шум печальный
Волны, плеснувшей в берег дальный,
Как звук ночной в лесу глухом.
Оно на памятном листке
Оставит мертвый след, подобный
Узору надписи надгробной
На непонятном языке.
Что в нем? Забытое давно
В волненьях новых и мятежных,
Твоей душе не даст оно
Воспоминаний чистых, нежных.
Но в день печали, в тишине,
Произнеси его тоскуя;
Скажи: есть память обо мне,
Есть в мире сердце, где живу я...
С такими начитанными людьми у Сергея и Михаила нет шансов.
Ну-да, ну-да... Потомки, "роющиеся в говне, быть может вспомнят и обо мне". Но Вам обоим не удастся втоптать в грязь гениальную мысль.
В чём, Виктор, гениальность? Если допустим Вы заявили: Согласно моим расчётам завтра в 12-00 пойдёт снег! На завтра ровно в 12 пошёл снег! То что пошёл снег - является достаточным основанием, чтобы считать Ваши расчёты верными! Это и есть проявление принципа достаточного основания! Теперь же, логики Сергей и Михаил делают такое "гениальное" утверждение : Отныне, Снег на улице будет идти исключительно на основании расчётов не менее гениального Виктора!
Понятна затея двух логиков?
Насколько я смог понять, то, что в данном случае Вы назвали "проявлением принципа достаточного основания", таковым не является. И Михаил достаточно подробно объясняет почему? Потому что между моим прогнозом в описанном Вами случае, и снегопадом "На завтра ровно в 12" нет никакой логической связи. Именно это я пытался Вам показать в Вашей теме про парадокс.
Не знаю что Михаил объясняет, но Сергей очень даже доходчиво объясняет и вот почему:
Улица для вас, Виктор, является одним из мест ("отраслью для синоптиков, например"), где вы получаете знания!?
И я с ним полностью согласен, теорема в одной теории, в другой может быть аксиомой.
Но Михаил говорит о логическом выводе. Логика не занимается прогнозами, с таким же успехом можно гадать на кофейной гуще.
Виктор, если Михаил говорит о достаточном основании как о логическом выводе (именно так следует вас понимать), а Сергей говорит по этому поводу о другом - основания берутся из других, с логикой не связанных, отраслей, То! Согласно закону формальной логики об исключённом третьем, один из них лжёт! Виктор, кто лжёт из двух логиков, Михаил или Сергей? (Хотя в вашем случае, Виктор, третье как раз дано - это вы сами)
Дискуссия Михаила и Сергея ещё не закончена. Мысль мне понятно, но в тонкостях я ещё не разобрался. Одно дело обкатывать метод, предложенный Михаилом, и совсем другое разбираться в теории. Вы же требуете категоричный ответ, которого у меня пока нет. И ещё один момент. Думаю здесь нет смысла делить мышление на онтологическое, научное, философское, человеческое, бесчеловечное. Логической верификации на полноту и непротиворечивость доступны любые тексты. Ну разве что кроме художественной литературы, которая по определению строится на противоречии, или конфликте.
Виктор, как это у вас нет ответа, если Сергей с Вами уже согласился! Не подводите коллегу!?
Согласился с чем? С тем, что нужно вникать в теорию? Вы же шпарите понятиями, а не однозначно определёнными терминами. У Вас же одни оценки, типа так не может быть, потому что не должно и всё!
И что интересно, Виктор! В результате парадокс был разрешён, а вы так и остались со своими "связями" на скамейке недовольных и возмущённых логикой!
Можно ссылку, интересно, что там за "коловративная фильтрация" :)
Посмотрите в "парадоксе" нашу дискуссию с buch !
!
Посмотрел:
Посмотрел:
Ну, и какое решение было, в результате которого разведены руки?
О каком решении Вы говорите, где ссылка?
vlopuhin, 28 Январь, 2021 - 15:03, ссылка
Начните отсюда: http://philosophystorm.ru/paradoks-2#comment-453777 и ниже, посмотрите, будет не понятно спрашивайте!
vlopuhin, 28 Январь, 2021 - 15:45, ссылка
.
http://philosophystorm.ru/paradoks-2#comment-455645
Согласен с Виктором. Но устал здесь бороться со школярским примитивизмом отождествления импликации с ЗДО, ответил общё в своей теме - ссылка.
Нет уж, Сергей, достаточно этого места, чтобы знакомиться с вашими бредовыми затеями!
Это у Вас конкретно логика ученого, и просто логика, разные логики. Согласно систематизированной символьной логики, логика либо есть, либо её нет. Причем эта система учитывает в том числе логику принятий решений, основанную на критериях: нравится, не нравится. Неадаптированные под суждения оценки.
Давайте теперь я свою оценочку вставлю. Мыслитель, который, после того как заявил, "Но это смех, а не достаточное основание", начинает утверждать, что он оперирует многоточиями, мыслителем не является. Это ниже уровня здравомыслящей женщины. Только совсем молоденькие девчонки играют в игру "Угадай чего хочу", оперируя как раз многоточиями, в виде продолжительных пауз.
Общеотрицательные суждения, это логика, поскольку учитывают квантор. На схеме они находятся как раз в штрихе шеффера на самом верху. Вам достаточно перевести дизъюнктивную форму, в форму импликации, чтобы понять, что это одно и то же.
А вот логика высказываний, которая кванторы не учитывает, это профанация логики. Вы можете сколько угодно в неё веровать. Но однозначно результата (1:0), она дать не может.
Я бы вам посоветовал не состязаться со мной в искусстве изящной словесности. Шансов у Вас нет. Твердый ноль.
Считаете что ЗДО не формализуем. Я вашу позицию понял. Не мешайте своей не обоснованной критикой тем, кто считает, что этот закон формализуем, разбираться в этом вопросе.
Слово "логика" употребляется и в таком значении, 2-е значение:
Аналогично - ссылка. Большой толковый словарь очень большой но у него нет ни глаз, чтобы читать наши сообщения, ни ушей, чтобы слышать. И зачем Вы такого третейского судью выбираете? Сами-то про логику что думаете?
Я объяснил, что употребил слово "логика" в словосочетании "логика учёного" во 2-м значении этого слова. Объяснил не вам. Если для оппонента нормы употребления слов, культура речи не излишество, он поймёт.
Но для вас, как видно, это излишество.
Аналогично.
В теме Система категорий (ч.31 ноологика -5) я показал, что современные философские исследования по логике давно превышают штампы, сложившиеся в школьных учебниках по логике и популярных заметках Википедии: гуссерлевская ноэматика, лосевсеая смысло-логика, моисеевская ПМО, моя ноологика и т.д. Но для Вас, наверное, читать нечто дальше Википедии - излишество. Извините, это не мой стиль письма, но Ваша грубость настраивает на соответствующие ответы.
Владимир. Из песни слова не выкинешь
"упрямый нрав моя беда, я свысока сказала нет - хотя шепнуть хотела да в ответ"
Если бы я девочку с таким строем мысли офлайн встретил, то с ходу бы сказал. Красивая ты конечно, но я не герой твоего романа.
Здесь другое дело.
В этом разделе, чтоб нивелировать флуд исходящий от Вас, я готов предложить вам почетную миссию лабораторной мыши, геройски пожертвовавшей своей жизнью на благо науки. Просто жертвовать Вы будете авторитетом 4 года 39 недель.
Мне очень нужен оппонент на котором я, без угрызений совести, буду демонстрировать непоследовательность рассуждений. Осталось добиться Вашего согласия. Это опыты над животными разрешены, без их согласия.
С другой стороны.
В основном пункте у нас разногласий нет. Мы с Сергеем хотим дальше формализовывать. А Вы можете отказаться от моего предложения без объяснения причин.
Сообщение ответа не требует.
Если не ошибаюсь, необходимо в верхнюю полуплоскость "перенести" квантор существования, ну что бы задействованы были все 16-ть булевых функций. Таким "посредником" может быть память. Иначе как в памяти смыслы не могут пересекаться. Если опять же не ошибаюсь, это называется типизацией данных, или переменных (если вам не известно что это, оценка, вопрос, императив, или утверждение, то вы не сможете корректно/адекватно ответить). Параллельные прямые параллельны на актуальной бесконечности, на потенциальной бесконечности они пересекаются, причем с двух сторон. Трансцендентное это то же самое что и материальное, только наоборот. Или то же самое - анти-ряд Дмитрия, с одной стороны законы сохранения (преобразования одного в другое), с другой - законы замещения.
Хотя я наверно чего то недопонимаю :)
логика=это лженаука . вот вы написали перед цитатой столько, что бедный студент и вправду поверит, в животворящую силу логики и самые способные понесут это знамя дальше, даже не спрося себя, а почему логиков не считают мудрецами и не прислушиваются к ним. в цитате. достаточно ясно просматривается необходимость ВИДЕТЬ ДЕЙСТВИТЕЛЬНОСТЬ чтоюы оценивать ПСС Природы, Т.е логики без действительности нет и только сама действительность и есть тот алгоритм , некоторые закономерности которого назвали логикой и носятся уже какое столетие с этим, как с писаной торбой, никакая логика не позволит выяснить от чего качаются деревья, надо встать с дивана и изучить явление, ВОТ СУТЬ, Все остальное словоблудие.
Мое предложение Владимиру остается в силе. О вашей персоне, я пока не думал. Даже сколько весит ваш авторитет пока не смотрел.
С Вас только согласие на участие в эксперименте. Будьте уверены, я уделю Вам достаточное количество внимания, чтобы Ваш авторитет сравнялся с нулем. Гарантирую.
Ну, если логику считать не наукой, то математику и подавно. Логика лежит в основании математики, а не наоборот. Просто, некоторые логики через чур самонадеянны, что ли? И в самом деле, высказывание : Если в огороде бузина, то в Киеве дядька, - так же является импликативным! С учётом всевозможных подсмыслов - эта импликация может быть как истинной так и ложной, а так же менять посылку и следствие местами!
И главное, что если даже в огороде не окажется бузины, а в Киеве окажется дядька, то и в этом случае импликация будет истинной, хотя посылка не включена в следствие! Спрашивается, где основания для следующей аксиомы?
Импликация истинна тогда и только тогда, когда посылка включена в следствие.
во -первых, нет ученой степени у нас в стране, как доктор мат наук, т.е уже все не так однозначно даже по формальным признакам. Но я привел этот довод не как основной , хотя он опровергает ваше утверждение.
Во вторых . в т.н. науке светской, нет оснований ни математики, ни логики, потому что она атеистическая, многим не видно , какие ошибки заложены в атеизме , потому объективных корней логики и математики они никогда не обнаружат.
В основании математики , в утилитарном смысле лежит простой опыт, как и в основании мышления, счет и потом арифметические действия, только по прошествии времени включились взаимосвязь, взаимозависимость и непротиворечивость, т.е все то, что лежит в любом размышлении правильном , не только в математике, никакой особой логики в математике нет, структура мат построений имеет все признаки системы и именно эти факторы плюс смыслы и есть те закономерности, которые заложены в устройстве Вселенной как организме-системе, имеющий смысл и методы, приводящие к нему. Вот основание и математики и логики, где математика средство алгоритма Мироздания, Творения.
Логика не может быть отдельной дисциплиной-это алгоритм всего, я и привел цитату в своем первом комментарии этой темы, где НАГЛЯДНО видно , что нет логики кроме действительности, причем автор темы сам подвел к этому, только не увидел всю бесполезность словесной околологической чепухи, тогда, когда надо просто оторвать заднее место от дивана и посмотреть , ЧТОБЫ СДЕЛАТЬ ВЫВОД, КТО ИЛИ ЧТО гнет деревья.
Ошибаетесь! Логика обращена к естественному языку - он же её основание! Математика вытекает из искусственного языка, потому и второстепенна по отношению к логике!
Знаете такую задачу: 2=1! -? (и кстати, почему в математике нельзя делить на "0"?)
"Математика вытекает из искусственного языка"
https://pearative.ru/stati/chto-takoe-zolotoe-sechenie/
Основание-это корни в природе.
сама математика от людей развивалась и как вроде бы независимые друг от друга направления, без связис действительностью, как казалось многим, так и с такими направлениями, где эта связь былавидна изначально, первые через некоторое время сталкивались с новым направлением, кото, уже требовало от них эту связь с действительностью устанавливать . Евклид и Риман, т.е в перспективе все будет связано и между собой и действительностью... и результатом и будет Математика от Природы как метапрограмма.
математика начинается с принятия счета (числовую последовательность) на веру? Так лучше?
Понятно, через тернии к заумным и мудрёным результатам!
В логике -главное :уметь признавать доводы и ошибки .
Вы написали что математика абсолютна искусственна, я привел вам пример-довод о математике гармонии, золотом сечении , где явно прослеживается связь с действительностью, ,
приводил и другие аргументы , где видна математика Природы
А в логике указали связь с каким то языком и , т.е приравняли логику только к словам, даже в этом случае гармония первична, учитывая атеистический подход эволюции , без инволюции, про остальное пока рано, с этим как...
Пифагор, если не ошибаюсь, вообще считал весь мир числом! Мало ли, кто что считает, важно понимать, как вы считаете!
Вот здесь, например:
, - ваше мышление обманывает вас! Но в силу своих предрассудков вы, Шадрин В.В., этого не замечаете!
Для тех, кто соображает в проблематике.
Верхняя часть - систематический каталог библиотеки булевых функций.
Нижняя часть - алфавитный каталог библиотеки булевых функций.
Стрелочки я убрал, чтоб не загромождали картинку.
а - частное, в алфавитном каталоге х, имена.
в - общее, в алфавитном каталоге y, свойства.
числитель - дизъюнктивная форма
знаменатель - конъюнктивная форма
Разбирать ребус нужно начинать с желтого квадрата. Это основа силлогистики.
значение 1/-А - не совместимы по истине, но совместимы по лжи.
значение А/0 - совместимы по истине, но несовместимы по лжи.
Сохраняю для истории. Вдруг благодарным потомкам понадобиться когда нибудь.
Сдаётся, что вы, Михаил, нам зубы заговариваете!? Импликативное (или условное) высказывание: Если в огороде бузина, то в Киеве дядька, - будет истинным, если в Киеве действительно окажется дядька, а бузины в огороде при этом не окажется! (То есть, следствие выполнено, при включенной ложной посылке.)
И наоборот: Если в Киеве дядька, то в огороде бузина, - импликация будет истинной в том случае, если в огороде окажется бузина, а в Киеве при этом не будет дядьки! (Следствие выполнено, при включенной ложной посылке.)
Что не так?
Операцию исключающего или нужно произвести. Она основание для действенности ЗДО. В матлогике это сложение по модулю2 крестик в кружочке. Там все просто.
У меня нигде не подразумевается: Или в огороде бузина или в Киеве дядька! Или Вы о чём?
Форма импликации.
в огороде бузина -> в Киеве дядька
Проводим операцию "исключающего или"
Существует в огороде бузина одновременно с тем что в Киеве нет дядьки? (1) В каком нибудь огороде она всяко есть, а дядьки в Киеве у владельца огорода нет. (истинно)
Существует в Киеве дядька, одновременно с тем что в огороде у племянника нет бузины? (1) По любому. У некоторых племянников Киевских дядек и огорода в помине нет, не то что бузин на нем. (истинно)
Две единички. Это горизонтальное деление квадрата Платона. Посылка и следствие не вкладываются друг в друга. Родовая либо видовая связь отсутствует. Связка импликации не обоснована. У ЗДО нет достаточного основания
В случае дизъюнкции.
в огороде бузина V в Киеве дядька.
Высказывание истинно.
Дизъюнкция истинна, если любая часть истинна.
У кого нибудь всяко есть в Киеве дядька (1) истинно. Вторую часть даже рассматривать не имеет смысла.
Я понятно объяснил?
Если предположению "в огороде бузина -> в Киеве дядька" на деле соответствует "в огороде бузина одновременно с тем что в Киеве нет дядьки", - то эта импликация будет ложной, а не истинной! (не выполнено условие!) Поясните, если не правильно понимаю!?
Тут, всё намного загадочней!?
У вас эта импликация "Существует в Киеве дядька, одновременно с тем что в огороде у племянника нет бузины? (1) По любому. У некоторых племянников Киевских дядек и огорода в помине нет, не то что бузин на нем. (истинно)" оказалась истинной, при условии что "Посылка и следствие не вкладываются друг в друга.". А как же, позвольте спросить, ваша аксиома, в которой условие истинности выполняется исключительно со вложенными друг в друга посылкой в следствие!
Я правильно понимаю вами, Михаил, изложенный материал?
Нет. Не правильно. Вы переключаете логический тумблер (1:0) посредством операции отрицания. Как это и принято в логике "импликаций" через закон исключенного третьего. А в этой системе он переключается введением границы. (^:v). Ближайший аналог, законы форм, или по другому законы именования Спенсера Брауна. Хорошие книжки. Много раз переиздавались, но оторваны от мат аппарата символьной логики.
Вот логический квадрат Платона с вербализацией значений. Нижняя часть под квантором существования, верхняя под квантором общности.
Для того, чтобы нижняя часть оказалась истинной достаточно одного примера исключения из правил. Существует ли хотя бы один прецедент? Типа ситуация с лебедями. Существование хотя бы одного черного лебедя опровергает аксиому, все лебеди белые.
Две нижние конъюнкции, соединенные через операцию дизъюнкции, вместе как раз дают таблицу истинности "исключающего или" сложения по модулю2.
Это правая нижняя часть квадрата. Конъюнкция, а не импликация. Мы проверяем саму возможность правомерного введения отношений подчинения. Ищем прецедент, способный опровергнуть аксиому. Черных лебедей ищем. Если найдем, хотя бы один огород, в котором растет бузина, но у владельца нет дядьки в Киеве. Аксиома будет опровергнута. Она не удовлетворяет условиям квантора общности. И конечно такой огород найдется. Поэтому (1)
Левая нижняя часть квадрата. Снова ищем прецедент способный опровергнуть аксиому. Таким прецедентом будет хотя бы один Дядька, и один племянник, у которого нет огорода, и соответственно бузины в нем. Таких дядек пол Киева. Соответственно тоже (1)
Квадрат под другие цели приспособлен. Семантические сети плести, но бузину с дядькой в общих чертах тоже решает.
Ну а поскольку в нижней части квадрата (1:1) то отношения подчинения мы в принципе не вправе рассматривать. Они не имеют достаточного основания. Это не связанные между собой посылка и следствие. Правомерно применять только связку дизъюнкции.
В огороде бузина или в киеве дядька.
Если в докторских диссертациях не проходящие проверку следовательно и потому-что на или поменять, вот фельетоны то получатся.
Банальности об ребусе импликации
Высказываю не свое мнение, а прочтете в любом школьном учебнике по формальной логике. Вы путаете причинно-следственное суждение с импликацией. Они по форме схожи, но по таблицам разные. Импликация, действительно, истинна если антецедент ложен, а консеквент истинен. Странно, но так в логике принято. Репликация, наоборот.
Над этой странностью, искусственно введенной, но тем не менее играющей колоссальную роль в логике и компьютерной технике, ломают голову не одно столетие. Вы бы вместо упрёков, предложили бы свой вариант объяснения этого ребуса.
Да ладно, что я могу предложить, если те "закорючки", - которые в массе своей использует Михаил - первый раз вижу.
Ничего такого я не переключал! Прошу, давайте обходиться без "закорючек".
Ещё раз и по порядку, если не против!?
Вот вами написано:
К этой записи я делаю свои замечания и пояснения. Вот они:
Что в моих замечаниях и пояснениях не соответствует вами изложенному?
Я подождал, чтобы Вы наговорили побольше, для ясности понимания, чего чему не соответствует. Я ж Вас за язык не тянул. Ловите щелбан. В этой теме правила простые - каждое Ваше слово используется против Вас. Надо думать, прежде чем писать - это осознанность.
Я пишу.
Привожу схему, в которой сможет сходу разобраться возможно только Виктор Лопухин, поскольку это машинная логика адаптированная под задачи органического процессора.
Отвечаете Вы.
По ходу дальнейшей дискуссии выясняется.
Я звал к обсуждению проблематики тех, кто соображает, а подключились Вы - который первый раз вижу.
Согласитесь, уже в этом есть что то мистическое. Читать же Вы умеете. Понимаете кого звали, и кто пришел.
Дальше Вы нашли себе товарища, который говорит многоточиями.
И воспользовавшись дружеской поддержкой договорились до
Я не мешаю. Держите тему в топе, с первой страницы не сходит. Я ж поглядываю. Уже здорово. Нахаляву типа трудоустроил двух попугайчиков. Работают на меня - время свое тратят (которое деньги).
Дальше я объявляю, что разговоры о теории мне не интересны.
На что Вы заявляете.
Ладно я побоку, мало чего мне, как автору раздела интересно, или не интересно. Молчу - значит побежденная сторона. Утвердились Вы в этой квартире.
Но самое главное, чьи затеи, в объявляете бредовыми. Идеи Сергея Борчикова.
Основания объявить затеи Сергея бредовыми, видимо те же. Не соображаете Вы ни в альфах, ни в омегах. В первый раз видите, как и в моем случае. А люди которые на переводы с древнегреческого время тратят, вообще лохи. Здесь же все понятно.
Основная тема, которая неожиданно вскрылась, это ФАНАТИЗМ. Откуда у Шарикова моральное право открыть рот, вместо того, чтобы по совету Преображенского молчать и слушать.
И еще нюансы. Почему здравомыслящая интеллигенция пасует. Ладно Сергей, он среди хоть как-то логически мыслящих людей обитает. Преподает.
Но и Виктор, который за словом в карман не лезет.
Это же мистика какая-то. Те кто имеют моральное право заткнуть Шарикова пасуют, а Шариков, который не имел морального права открывать рот, делает свои глубоковысосанные из носа оценки, и самое нелепое, побеждает. (я переношу проблематику из практического занятия "мораль", мы ей как раз сейчас на практике занимаемся)
Нужно приглашать мистиков. Без них не разобраться.
Кто то изучает Гурджиева по Успенскому, хотя тот самостоятельный мистик. Но Непредвзятый свидетель Питерс Фриц, куда доходчивее.
Проблематика пересекающаяся. Но парадоксальная. Желуди не ставшие дубами просто гниют и становятся удобрением. А Шариковы, не дают развиваться другим, поскольку почетная должность удобрения это то, к чему они принуждают других согласно своих оценок того, что возможно или не возможно.
Откуда Шарикову знать, что возможно, а что невозможно. Если он.
Может подучиться Владимир!
Некоторое время помолчать и послушать? Выбрать онлайн курс, которому Вы доверяете, и разобраться с символьными записями используемыми в мат логике. Тогда это будут не закорючки а аналоги (=,+,-,/,*)
Математические действия скорее всего для Вас не закорючки. Это же любой знает, кто в школе учился. А логические (v,^,-,->,<-)- закорючки. Может дело не в закорючках? А том, что подучиться надо, перед тем, как свои глубокровысосанные из носа оценочки предъявлять.
Проблематику то Вы серьезную вскрыли.
Чувак, который прет в метро обвешанный взрывчаткой, тоже запросто заявит. Я иду в рай - скажите, где я не прав. Мне же дядьки авторитетные обещали, что я в Рай прямой дорогой иду.
Возвращаемся к началу.
Еще раз уточните, что в моих исчерпывающих пояснениях Вам не понятно.
Но помните. Каждое Ваше необдуманное слово будет использовано против Вас.
Что называется Кормин разгулялся в своей
комнатетеме!Вам же, Михаил, ясно всё изложили в прошлый раз! Что Вы переспрашиваете как тугоухий?
Ожидаемая еврейская проблематика. Отвечаем вопросом на вопрос.
Разбираем по пунктам.
Фиксируем начальные условия.
Авторитет Владимира из Смоленска 2 недели и один день. Фирма однодневка.
Да это даже хорошо. Перелогинитесь Владимир и ничего не потеряете. У меня все моральные обязательства теперь по отношению к вам сняты. Буду гнобить по черному. Как и полагается поступать с Шариковыми, которые суют свой сопливый младенческий нос в проблематику в которой они
Даже если Вы в следующий раз представитесь Авраамом из Авраавмовка, я Вас вычислю по набору букв. Такую бредятину сложно не отличить от осознанных текстов. И снова засуну ниже городской канализации, где Вам и самое место. Шариков должен молчать и слушать. Молчать и слушать. Киношку "Собачье Сердце" пересмотрите перед тем как в следующий раз лезть со своими глубоковысморканными выводами на ФШ.
Чего тут не понятного, для человека который в русском языке соображает. Связку подчинения применять логически нельзя, только связку или.
Но вы ж то применяете! Как Наполеон из Кащенко, который разложил по методу Задорного НА Поле ОН. Типа мама мне говорила, что в поле родила, и все время причитала, ОН чего приключилось. Значит НА ПОЛЕ ОН, эжто Я.
Давайте еще раз по полочкам вашу бредятину кащенковскую разложим.
Откуда взялась связка подчинения? Я в предыдущем тексте внятно сказал, что именно она, и не обоснована. Можно только "или" применять в логически связной речи. Вы же желаете заострить внимание на своем логически несвязном мышлении. Какое нафиг условие может быть не выполнено в ваших кащщенковских фантазиях. Там все условия выполняются априори. Чего пациент замечтал, за то и морду соседям по палате бьет. Мораль высокая, но такая вот собачья. Лаять позволяет, а думать не обязательно
Я вам про конъюнкцию, Вы тут же переименовываете её в импликацию, поскольку образования, позволяющего отличить одно от другого, нет. Зачем открывать свой необразованный рот, на философском форуме?
Владимир. Это чисто прививка. Я еще даже на полпроцента не разогнался в искусстве изящной словесности. Если Вы не стекаете с моего раздела сверкая пятками, я вам запросто инфаркт микарда, вот такой рубец организую. И совесть моя будет чиста яки у младенца. Я ж всех предупреждал не флудить в моих темах. Здесь у меня будка и цепь.
Текайте уже.
Сообщение ответа не требует.
Тут ничего не скажешь, уникальный самодур и его предостаточное основание:
Я никогда и не отрицал, что я самодур.
Только Вы один об этом не знаете в силу своего младенческого опыта на ФШ. Прямым текстом всегда пишу.
А Вы, Владимир, кроме Неуча, еще и ссыкун знатный. На такое сообщение объемное только одну строчку своих высморков интеллектуальных для моей критики предоставили. Но я все равно нашел чего покритиковать.
Бегите уже отсюда, и не попадайтесь мне на глаза. Ссыкунов я еще больше чем Шариковых недолюбливаю.
Ну раз самодур, значит и ссыкун и неуч заодно!
Вот видите, Владимир, Ваши сообщения становятся все короче и короче. Правильно мне бабушка говорила. "Воспитывать детей без розги, брать грех на душу". Тень разума в вашей кащенкосвкой головушке замаячила.
Вы понимаете, что значит в логике это импликация?
Давайте я перепишу для ваших младенческих мозгов.
самодур -> ссыкун ^ неуч.
Посмотрите на формулу и осознайте, какой бред у Вас в головушке небитой.
А... Вы же в символизациях не соображаете. Но люди то, которые нашу квартирную склоку читают - соображают. И мотают себе на ус. Все что сказал Владимир Р из Смоленска 2 недели и один день от роду на ФШ нужно делить на 16. Делить нужно, поскольку он не ведает, о чем трепится. Трепач - Владимир Р из смоленска!!! Кроме того, что он ссыкун и Неуч который сует свой нос в темы которые он в первый раз в жизни видит.
Вот так Авторитет и уходит. Смотрите сколько я Вам ярлыков обоснованно навесил. Я ж препод на пути кривды. Вы с кем скалиться вздумали - мальчуган.
Бегите.
Конечно вижу, не только короче, но и заметно уже! Уверен, Ваша бабушка была благочестивой, невинной женщиной: Порола Кормина Михаила как сидорову козу!
Попытка разбора схемы М.Кормина
То, что 2 элемента по 4 составляют 16 комбинаций, банально, не обсуждаю.
То, что эти 16 комбинаций могут быть как-то поименованы и выражены через логические функции закономерно. Имена авторов одних наименований теряются в веках, других - закреплены в названиях (Пирс, Шеффер). Тоже не разбираю.
Представляет интерес, как эти 16 увязаны между собой – логически и логико-семантически. Я думаю, таких схем и моделей может быть предложено разными логиками тоже немало. Пусть логики и читатели ФШ поломают над этим голову. Я же ближе к теме ЗДО.
Учитывая, что половина функций зеркальна (зеркальные пары обозначены на схеме линиями-связями сверху), т.е. просто 0 заменяются на 1 и наоборот. Остается уникальных 8 столбцов, и у меня поначалу появился соблазн увязать их через восьмиугольник. Но в него никак не вписывались 6 комбинаций (обозначенных снизу красными треугольниками), которые по сути не функции, а лишь величины.

По этому же пути пошел и М.Кормин. Он просто абстрагировался от этих 6 величин, а из оставшихся 10 (8) собрал восьмиугольник. Правда, две величины – строгую дизъюнкцию и тождество (красная связка сверху) – пришлось вводить внутрь многоугольника, им вершины не нашлось.
И тогда эти 8 вершин, поскольку они зеркальны, оказались попарно зеркально симметрично расположенными на противоположных концах восьмиугольника. Здесь ничего сложного не вижу, элементарная комбинаторика.
Изюминка заключается в том, что почти все функции коммутативны, т.е. от перемены места х и у они не меняются. А лишь четыре представляют обратные функции (обозначены синими стрелками-связками снизу). И вот эти-то функции оказались на вершинах восьмиугольника, через одну, образуя так называемый М.Корминым квадрат Платона. Но если запрет х и запрет у (нижняя сторона квадрата), на мой взгляд, никакой эвристической силы не имеют: так, формальность. То вот обратимость импликации и репликации (верхняя сторона квадрата "Платона") призвана сыграть самую что ни на есть сущностную (истинностную) роль во всей мировой логике.
Именно она, да еще усиленная располагающимся на ней законом тождества (зеркальностью строгой дизъюнкции) и призвана обеспечить функционирование закона достаточного основания, а следовательно и истины.
Вербальное определение формулы ЗДО – закон достаточного основания есть дизъюнкция импликации и репликации.
В матлогике все эти функции коммутативны. Коммутативны они потому, что математика не реагирует на качество. Все числа одного качества. Предложенная система реагирует на качество переменных по порядковому номеру в формуле. первое - всегда имя, частное. второе - всегда свойство, общее
Это математизация логики Спенсера Брауна. Здесь различаются имя и свойство. Переключение (1:0) происходит не посредством отрицания, а посредством введения границ. (^:v). ^ - отсутствие границ между переменными, v - наличие границы между переменными.
Система начинает различать.
Философия истории (х^у) - ссылка на базу данных по нужному адресу.
История философии (у^х) - ссылка на базу данных по нужному адресу.
Это переворот не в логике, а в информатике. Причем глобальный переворот, круче чем переход с ламп на полупроводники. Я же обещал Виктору vlopuhin, создать базу для электронного переводчика, который сможет переводить с фени на церковнославянсткий. Я её сделал. Машина теперь способна различать не только количество, но и качество.
Нет Сергей.
Закон достаточного основания, это правомерность введения квантора общности через импликацию, репликацию, либо эквивалентность посредством двоичного кода операции строгой дизъюнкции.
х у +
0 0 0 - правомерно через эквивалентность переменных
0 1 1 - правомерно через репликацию
1 0 1 - правомерно через импликацию
1 1 0 - не правомерно
Как Вы надеюсь понимаете, Сергей, квантор общности, это и есть закон. А результаты обработки баз данных в виде таблицы истинности "исключающего или" достаточное основание для него. Закон достаточного основания, это закон законов, во всех возможных мирах.
Я не нашел способов сделать людей умнее, поэтому ищу способы сделать умнее планшеты, которые, вместо нас, учат наших детей.
Но попытки сделать людей умнее я не оставил. Этому посвящены последние темы Виктора. Как то мне удалось его уговорить.
Мышление, или при чем здесь логика?
Что такое право?
Мышление, или при чем здесь логика? 2
Что такое мораль?
Там на практике обкатывается именно то, что здесь изображено в виде безличных теоретических схем.
Уважаемые посетители моего раздела. Я всех вас приглашаю на практические занятия. Мне не интересно говорить о теории. Вот там, Вы на практике и покажете глубину своего УМА.
Критиковать уже сделанное не имеет смысла. От Вашего мнения ничего не зависит. Время само все расставит на свои места. Не захламляйте раздел пустыми комментариями.
Мне нравится сама идея найти формальное обоснование ЗДО, и я с удовольствие посмотрел ход мысли, но обращу ваше внимание на то. что даже википедия подчеркивает тот факт, что
Если "обнажить" эту мудреную мысль, то очень просто - речь идет о неком содержании, которое, как правило, эксплицитно не выражается, но имплицитно присутствует...
Но я несколько о другом... Я обратил внимание. что в западной философии этот принцип (ЗДО) практически не упоминается именно в силу выше-сказанного. А эта тема, ИМХО, стала фигурировать под темой "Фундаментальность".
Дам ссылку, наиболее известного автора данной темы и понравившейся мне статьи:
Fundamentality and Ontological Minimality (Tuomas E. Tahko (University of Helsinki))
https://www.academia.edu/21867745/Fundamentality_and_Ontological_Minimality
Что бы яснее стало, приведу оттуда абзац:
О чем вообще речь? О том, что мир системен (технология "одно"-"многое")! Мереология - это один из способов выражения системности.
***
У вас в статье:
А что значит это на онтологическом уровне? Ну, например, с позиции мереологии (части и целого)? Вот эта фраза: "посылка включена в следствие"? А то, что "посылка" это "часть" "следствия" как "целого".
Да, я понимаю, что когда мы говорим "металлы электропроводны", то следуя традиции, легче это представить в терминам "субъекта" и "предиката". Но вы ведь пользуетесь диаграммами Вена? Уже разбиваете на "части"? ... значит речь идет о некой форме абстрактной выразительности?
Вот мереология, по мнению некоторых авторов, наиболее выразительна в поисках фундаментальности, поскольку совпадает с существующим концептом системности.
***
Как по мне, исходя из вышеизложенного, ЗДО сводится к онтологическому минимализму - непротиворечии системности. Собственно, по такому пути и вы пошли, только в другом исчислении (насколько я помню, такое предикатное исчисление исключает иерархию (поправьте если что), а принцип фундаментальности его предполагает исходно.
ИМХО!!!
Не знаю, ответит или нет Михаил, но я ответил - ссылка.
Я не исключаю иерархию Виктор. Я просто логически непротиворечиво складываю пазлы. А уж что там проявится, иерархия или анархия, только программисты докажут. Когда соберут ядро операционной системы на основании "и", "или". Опора на эксперимент приветствуется. Я уверен, что эта операционка будет на порядки производительней, но это мои считалки. Опыт все сам расставит на свои места.
Смотри ка, не думал что и в Википедии найдутся разоблачительные статьи в адрес самонадеянных авантюристов Михаила и Сергея, которые за своим крючкотворством мнят себя мучениками науки!
Ну щас я сыграю доброго следователя :)
Википедия это не только хорошо, но и плохо. Это большая, я бы сказал всемирная, помойка, по этому на ФШ приводить статьи из Википедии в качестве аргументов не принято, только в особых случаях, грубо говоря когда уже не только переварено, но и впитано.
Но это так себе, лирическое отступление. Кажется я понял в чем так сказать камень преткновения. Проблема известная - пропасть между теорией и практикой. Можно сказать и так: в теории говорится как и из чего строить, на практике строим как можем и из того, что есть. Но и это не всё, вспоминаются наши дискуссии с Дмитрием (Dimitro). Пример из математики. Прежде чем решать задачу, необходимо иметь оценку, имеется ли вообще у этой задачи решение? Этот момент зачастую упускается, а зря. У Михаила с этим как раз всё в порядке:
Этим сразу была отсечена та проблема, которую здесь широко муссируют Владимир Р и Владимир К. Дело в том, что согласно теоремам Гёделя полными и непротиворечивыми могут быт только формальные системы, такие как, например, арифметика. Затем последовало ещё одно уточнение:
Теперь становится понятно, что моё сравнение таблиц истинности с трещинками на потолке неуместно. Да, в аналоговой технике всё не так, картинки кистью намного богаче компьютерной графики квадратиками, но речь то не о них! В общем случае наука это система из эмпирических знаний и теории, в ней полнота теории обеспечивается за счет противоречий системы! Но ведь это из другой области, тема Михаила о другом. Мало того, он неоднократно и каждый раз всем это повторяет.
Но вернёмся к теме. Вот что пишет Сергей Борчиков:
Ну то, что извратили и проигнорировали понятно, что ещё от них ждать? Меня заинтересовало другое. Почему у Сергея одно выражение (одна строка), а у Михаила два? Потому что все логические объекты ходят парами. Например, если определились со сложением, то непременно вылезет проблема с вычитанием, и для вычитания придётся строить свой алгоритм. Другими словами любой закон в логике будет иметь две стороны, если это закон тождества, то обязательно есть закон не-тождества. У Михаила закон достаточного основания сразу идёт из двух выражений, потому что иначе никак, он на стыке теоретической и прикладной логики, более того опирается на аксиому. Откуда спрашивается аксиома? Из философии! То же самое с теоремами Гёделя, их две, и они доказываются не строго в математическом (формализованном) виде. Как любит выражаться Владимир Р, теоремы Гёделя не референтные.
Тогда почему у Сергея одно выражение? Мне кажется будет понятно на образном примере. Все видели параболу? Разбиваем её горизонтальными прямыми. Владимир К и Владимир Р бьют в пустоту. Сергей попадает в одну точку - точку экстремума. Михаил разбивает параболу на две части, то есть его прямая пересекает параболу в двух точках, отсюда и два выражения.
Вывод теоретический: как не может быть философии без логики, так и логики без философии. Вывод прикладной: логика и мышление это "две стороны одной медали".
Вы не следователь, vlopuhin, а адвокат двух мошенников, чей блеф был вскрыт безо всякой Вики-Пики-Пети!
А "муссируют" Владимир Р и Владимир К только одно: кому из этих двух горе-логиков Сергею или Михаилу бежать за ящиком минералки! Их от всемирного позору спасают, а они тут возмущаются и морщатся!
Мне иногда нравится художественно литературный жанр, но это не тот случай. Не поверите, у меня даже одна коза рисовать умеет. Берёт в пасть соломинку и водит ей по стенам. Первый раз, когда я это заметил, подумал случайно, но это повторилось несколько раз. Буквально вчера я ей сам дал соломинку в пасть, и она повторила свой "подвиг"! Теперь даже не знаю, что с этим делать... :)
Виктор, тут главное не растеряться! Купите силиконовый палец и дайте вашей козе! Пусть она за вас сообщения набивает!
Вы не поняли. Открытым текстом: я не буду больше отвечать на Ваши комментарии, что бы не давать Вам повод бздеть не по делу.
Разоблачать мошенников - это по вашему бздеть не по-делу?
Вас же предупреждали, здесь не мошенники, здесь цепные псы, правда пока сидят в будке, никого не трогают, но могут и откусить чего нибудь, по самые уши :)
Виктор, вы считаете что Сергей и Михаил - это псы, которые сидят на цепи и в какой-то там будке? Тогда не понятно, кто пишет за них сообщения? Поясните?
Шутки шутками, но меру всё же надо знать. За мошенников советую Вам извиниться, и дальше развивайте эту хрень без меня.
Замечание по существу! Спасибо, Виктор! Действительно, это не просто мошенники - это интеллектуальные мошенники! Прошу прощения за неточность!
Эти формулы за уши притянуты.
В книге И. Демидова "Логика: Учебное пособие для юридических вузов" приводится схема:
"А есть потому, что есть В", а если В нет, то и А нет. На нет и слов нет.
Есть В - логика имеет место, нет В - логика не имеет места.
У вас есть деньги - вам есть на что существовать. Нет денег - существовать вам не на что.
Какая здесь может быть формализация?
Это Вы "притянули за уши" причинно следственную связь (ПСС) туда, где ей нет места. Можете пообщаться на эту тему с Александром Болдачевым, типа женился потому что купил цветы по дороге в ЗАГС :)
Предметно вы не возразили.
Кстати, причинно-следственная связь формулируется самим законом.
Вы считаете предметным возражением ссылку на авторитетное издание? По Вашим же заявлениям необходимо разбираться что это за А и В, из какой области знаний, вдруг накосячили...
Я считаю правильным, потому привёл.
Что касается А и В, то здесь всё просто -
Сущность закона: всякая мысль (А) может быть признана истинной только тогда, когда она имеет достаточное основание (В), всякая мысль должна быть обоснована.
Так всё таки это про мысль с её логическими связями, или про вещдоки с подозреваемыми и преступниками? Вы уже как нибудь определитесь, за какой Вы "Интернационал"?
Если достаточным основанием является факт, то он не сам по-себе является достаточным основанием, а является достаточным основанием как осмысленный факт - как мысль о факте. И так со всеми достаточными основаниями.
В схеме автору это нужно сообщить и он пишет:
Теория не оперирует фактами, ей аксиомы подавай. Любой факт может быть истолкован как в доказательство, так и в опровержение любой теории.
Можете сколько угодно разглогольствовать о теории, а я придерживаюсь этого -
Тут как говориться, если факты противоречат "закону достаточного основания" двух авантюристов, то тем хуже для фактов!
Почему двух? Здесь ещё третий дерзает.
Не думаю, что Виктор должен участвовать в поставке ящика минералки!
Я в одинокого вывезу. Ну что, борцы за правду, поиграем в каламбуры. Ума вам бог не дал, так может вы хоть как стартаперы тянете.
Мы сейчас на практическом занятии "мораль" проходим. Очень интересно узнать.
Вы чего тут до сих пор третесь Владимир Р, если я Вам уже три раза на дверь указал? Где истоки правды, за которую вы репутацию условно приличной девочки Владимир К, на кон в игре поставили?
Да мало ли дурочек по свету ходит в майках, с надписями "я не легкомысленная, я доверчивая" и многоточиями разговаривают.
Это у вас здесь ни друзей ни репутации. Две недели стаж на форуме. У девчонки Вашей 4 года и 39 недель на кону.
Я вас заткну, и вы слиняете. С темы моей точно, а возможно и с форума. А девчонке то вашей чего потом делать? Как оправдываться? Зачем она с прохиндеем связалась, который поматросил и бросил.
Вы вообще чувствуете ответственность за тех кого приручили Владимир Р?
Основной вопрос.
Что вас заставляет Владимир Р, не имя никакого авторитета за спиной, жертвовать репутацией доверчивого человека, у которого этот авторитет имеется?
У вас потому, Кормин Михаил, репутация подмочилась, что вы только о ней и думаете, а не о принципе достаточного основания.
Ответ то на вопрос ГДЕ?
Это же вы Владимир Р - как раз тот червяк смрадный, который на доверчивых людях себе авторитет без всяких оснований заработать пытается. Вы на вопрос ответьте, хоть что нибудь. Блесните уже мыслью своей. Девчонку свою (Владимир К) порадуйте. Чтоб она осознала, что не прохиндею, а гению доверилась.
Я понимаю, что бог вам ума не дал. Поэтому второй раз вопрос повторяю.
Поверьте, Михаил, на ваши глупые вопросы никому кроме вас и не ответить:
Вы зачем мое имя над своими детсадовскими компиляциями вставили? Это чего реально предел фантазии? КТО ОБЗИВАЕТСЯ, ТОТ САМ НАЗИВАЕТСЯ? Место вам в детском саду пироженки из песка лепить, и обсуждать со сверстниками, чей папа сильнее.
ПОДИТЕ ВОН ИЗ МОЕГО РАЗДЕЛА!
Мыслитель - детсадовского уровня.
Сообщение ответа не требует.
Понимаю, минералочки от вас не дождёмся!? или что?
Вы это математикам расскажите, как так они, суки такие, без яблок, счетных палочек и землекопов свои дерзкие теоремы доказывают :)
И кстати повторюсь, ничего страшного, закон Ома был получен эмпирическим путём, а потом выведен из уравнений Максвелла, по крайней мере на уроках физики в школе :)
Математика - наука о цифрах, а не о землекопах и ... !
Логика - наука о мышлении, а не о явлениях в действительности!
Было же условлено, как только Михаил и Сергей отождествят явления в мышлении с явлениями в природе, так я первый кто принесёт им ящик минералки с глубокими извинениями!
Назовите хотя бы один закон науки математики.
Наслаждайтесь!
Переместительный закон сложения цифр, а не землекопов!
Сочетательный закон сложения цифр, а не и т.д.
Переместительный закон умножения
Сочетательный закон умножения
Распределительный закон умножения
Сложение цифр обсудите на досуге с Владимиром К, но здесь потрудитесь, пожалуйста, объясните уважаемой публике, что такое
?
Круто! Конечно, объясню!
под ", а не и т.д." необходимо понимать то и только то, что соответствует смысловому ряду vlopuhinа - "а не яблок, счетных палочек и землекопов!
Повторяем еще раз, при этом стараемся, чтобы ребенок участвовал в проговаривании объяснении, повторял за вами. Затем кладем перед ребенком...
Да, Виктор!??? Вам компот надо было яблочный варить ещё осенью, а не теперь зимой! Чем думают эти философы, яблоками в голове, а не на снегу! Виктор, признавайтесь, у вас яблоки в голове?
Не правильный ответ. Подумайте ещё. Подсказываю, это не про кулинарные рецепты.
Нет, это именно про кулинарные рецепты вашей логики!
У тю-тю-тю-тю-тю-тю!
Это написал -
Поди он от математиков скрывал, той же академии.
"Абсолютно здоровых не бывает, бывают недообследованные."
Дамаю я уже достаточно из вас признаний вытянул. Покедава, мне пора на вечернюю дойку :)
Виктор Борисович, очень интересное у Вас сообщение (ссылка) с попыткой объяснить, почему в формулировке ЗДО у М. Кормина две формулы, а у меня одна. Но ответил на него (и получилось достаточно объемно) в параллельной теме – ссылка.
Здесь же, в текущей теме, работать трудно, поскольку она подверглась атаке троллей. У Михаила еще хватает сил с ними бороться, а Вы – добрейший человек. Хотя впрочем у модератора всегда есть средство, предоставленное правилами форума: «Чик» – и нет троллей.
Простите, Виктор, а вы случаем не тот Виктор с Феномен.ру, который всячески популизировал Википедию!?
Нет. :)
Спасибо, за ответ! Извините, уж больно стили "широкой" аргументации похожи!?
Опять не правильный ответ. Даю ещё одну подсказку. Смотрите внимательно, я даже подчеркнул нужное:
говорите, Виктор, по существу, а не абы как..
Объясните, почему "не"? Почему не "и", конъюнкция:законы сложения и цифр, и яблок, и счетных палочек, и землекопов? Картинка с яблоками Вам в помощь. Или Ваш компаньон поможет? Как там у вас с взаимовыручкой, сможет он опуститься до такого уровня?
Я так понимаю.
Вот чего вы хотели -
Вам назвали пять. У вас по ним вопросов нет. Но желание есть, "придратся к фонарному столбу".
Вы же вроде на академиков привыкли ссылаться? Источник смотрели, откуда законы взяты? Беспорядочные связи до хорошего не доведут, я там авторов не нашел, даже "лицо побить" некому... :)
Спохватились! Но претензия не ко мне, не я вам "наслаждение" доставлял.
Что значит спохватился? Это Вы опустились с академического до детсадовского* уровня, фраеров ищите где нибудь в другом месте, что бы им порожняк с законами математики гнать.
*Это даже не детсад, и не дурдом, в одном хотя бы дети нормальные попадаются, в другом санитары, это мрак полнейший.
Нет, Виктор! Ничего вам объяснять не буду! Вы долго сражались с парадоксом Сократа и Платона, и в результате парадокс Платона и Сократа вас одолел! Но даже этого вы не осознали! Вы, Виктор, человек глупый, хотя наверное и хозяйственный!
Очнитесь, Володенька, какой Платон, какой Сократ?... Вам для начала с яблоками разобраться край как необходимо. Когда разберётесь с яблоками, можно будет переходить к цифрам, если и это осилите, в чем я сомневаюсь судя по этому - ссылка, можно будет и о числах думать.
И не ждите, что кто то за Вас это сделает, напрягайте собственный моск, как говорит Эрц, не бойтесь, он не сломается, поскольку дер нематериальный. Хотя... Кому я это говорю?...
А что тут разбираться и так понятно! Бывают яблоки на снегу, а бывают яблоки вместо цифр у Виктора в голове - розовые в сером веществе!
Опять неправильный ответ. Сосредоточьтесь, Владимир, но не на мне, моя личность Вам только мешает, а на яблоках. На картинке, которую я Вам подкинул, таблица истинности сложения двух чисел 1 и 1, и не важно чем её заполнить, цифрами ли, счетными палочками ли, землекопами ли, но удобнее яблоками, круглое катать удобнее. И запомните, в математике нет законов, в математике формализуются законы природы, то, что Вы привели выше, это основания математики, или аксиомы (ну это для тех, кому эти аксиомы доказывать лень). Можете не отвечать, я больше не читаю Ваши комментарии.
Да, это как один еврей писал письмо другому еврею. Вот он пишет в конце:
Абрам очень хотел послать тебе сто рублей, но извини, уже заклеил конверт!
Вот ведь мексиканец неубиваемый, из Джека Лондона. Три раза указал на дверь, один раз конкретно выгнал вон. А вы, Владимир, все трындите, то про минералку которая предвкушалась, то про евреев которые причудились к месту.
Я тут для Болдачева статистики подсчитал. Пусть пересчитает, если не верится.
на 15.20 по ФШашному времени 31. 01. 2021 в теме 167 комментариев.
из них явное лидерство у вас Владимир Р - 56 шт, не смотря на то, что в проблематике "первый раз вижу" и мышление детсадовца из песочницы.
Ваша подружка Владимир К, которая на третьем месте имеет статистики - 22 шт. В голове ни бум бум малолетка дура дурой, слегка отстает по производительности.
Я на втором месте 26 шт включая старт топик и этот комментарий.
Если сложить ваши статистики 56+22 = 78 шт
Вы вдвоем написали в три раза больше чем я один. Но я ж то не только вам отвечал. Я всем участникам обсуждения уделил внимание.
Я у Болдачева на карандашике. За словом в карман не лезу. Закусились мы совсем недавно. Он всяко теперь читает, чего я пишу. И этот ком тоже всяко прочитает.
Теперь следите за мыслью. Мне выгодно когда вы, без устали, пишите всякий бред в моей теме. Тема держится в топе. А людей, сюда пришедших, я отправляю в параллельную тему Сергея. Мне пофигу где обсуждать. В теме
http://philosophystorm.ru/sistema-kategorii-ch25-2-zakon-dostatochnogo-o...
У вас шансов нет. Чикнет Сергей маленькой красной кнопочкой, и нет мексиканца. Как там в песне Одесского шансона поется.
Но спор в Кейптауне
Решает браунинг,
И англичане
Начали стрелять.
Но я этим путем идти не хочу. Есть у меня маленькая красная кнопочка, и право ей пользоваться есть. Сергей мне на это право намекает.
Право удалить ваши, Владимир Р, комментарии у меня есть. А вот желания их удалять, у меня нет. Это мое право, пользуюсь по желанию и в соответствии с собственными принципами.
А Вот у Болдачева теперь моральная проблема. (мы мораль на практике проходим, переношу сюда практическую проблематику). Он же модератор. Бан, отъявленных тролей, которые гробят имидж ресурса, где он числится модератором, для Болдачева уже не ПРАВО, а ОБЯЗАННОСТЬ. При чем у Болдачева Жирная красная кнопка, которая забанит вас всерьез и надолго, не только в моем разделе, но и на всем ресурсе ФШ.
Я жду и считаю, сколько раз Вас, Владимир Р, нужно откровенно выгнать ВОН из моего раздела, чтоб корпус модераторов ресурса начал заниматься своими непосредственными ОБЯЗАННОСТЯМИ.
Такие у меня принципы. Я за монополию насилия на конкретной территории. Самосудом не занимаюсь, и жалобы писать в падлу. Подрядился Болдачев на модераторский пост в иерархии небожителей ФШ, соответственно Вы, Владимир, его проблема, а не моя. Мне Вы только пользу приносите - тему в топе держите.
Я вам обещал роль лабораторной крысы - вот она, на блюдечке с голубой каемочкой. Здесь серьезные люди с взрослыми мозгами интригу держат. А ваша лабораторная судьба никого не интересует. Тем более авторитет у вас уже отрицательный, а не нулевой, как было изначально.
Ну что еще сказать на последок.
ПШЕЛ ВОН ИЗ МОЕГО РАЗДЕЛА - ИНТЕЛЛЕКТУАЛЬНЫЙ НЕДОНОСОК,
Кормин Михаил, скажите, вы не нормальный!? Удалить можете и не можете!? Вы не нормальный?
Я принципиальный, и принципы у меня свои собственные, а не нормированные. Соответственно я не нормальный, а принципиальный.
Давайте еще разок для статистики закрепим.
ПШЕЛ ВОН ИЗ МОЕГО РАЗДЕЛА - ИНТЕЛЛЕКТУАЛЬНЫЙ НЕДОНОСОК,
Всё нормально! Вы не нормальный, Кормин Михаил!
Вы снова, по своим детсадовским понятиям, исказили мою цитату, в надежде, что никто не заметит.
Следите внимательно. Я написал.
А вы, как заправский журналист, тут же переделали.
Причем ссылочку на первоисточник убрали. Это в тренде журналистики, но они хотя бы стартаперы в основной массе. Вы в этой области не тянете. Я проверял.
К моим обоснованным ярлычкам к вашей интеллектуально недоношенной персоне, я теперь могу обоснованно добавить еще один.
Раньше я писал.
А теперь у меня есть обоснованное право сказать, что владимир Р (с маленькой буквы пишу, большой вы уже не достойны), кроме того, что он трепач, ссыкун, и неучь, еще и откровенный лжец и подтасовщик.
Моя аргументация основывается на истории ваших сообщений. (которую вы стереть не можете, поскольку раздел мой)
Давайте еще раз повторим для статистики.
ПШЕЛ ВОН ИЗ МОЕГО РАЗДЕЛА - ИНТЕЛЛЕКТУАЛЬНЫЙ НЕДОНОСОК,
Ярлычки у вас, Михаил, действительно были недоношенными, а теперь правильные!
Не понимаю. Логический квадрат Аристотеля это силлогистика, а не логика предикатов. В силлогистике SiS аксиома. В КЛП SiS не имеет смысла, как я понимаю.
Тема подверглась атаке троллей, а мне мои внутренние принципы не позволяют удалять комментарии. Последний мой комментарий в обсуждении которое открыл Сергей Борчиков.
Кормин Михаил, 31 Январь, 2021 - 09:32, ссылка
Формализация логического закона достаточного основания
Интересная разработка. Очень интересная! Жаль, что летом эту тему как-то пропустил. Но по ходу дела выскажу пока одно соображение и один вопрос.
Во-первых, на мой взгляд, неплохо было бы разграничить понятия "формализация" и "экспликация". Последняя есть просто уточнение формальными средствами некоего концептуального содержания.
Например, тот же закон достаточного основания (ЗДО) можно эксплицировать даже посредством логики предикатов - прикладным образом, введя некоторые интенсиональные предикаты. Тогда ЗДО можно представить в виде прямой импликации ∀х(Е!(х) → О(х)), где Е! - предикат сингулярного существования, а О - предикат "быть основанием". Отсюда путём чисто формальных преобразований можно вывести некоторые следствия - например, ¬∃х(Е!(х) ∧ ¬О(х)), т.е. нет таких вещей, которые существуют, но не имеют основания. Заодно обозначается проблема определения универсума пробегания кванторов, которая в содержательной формулировке ЗДО как бы теряется на заднем плане.
Но у Вас больше, чем просто логическая экспликация - попытка именно формализации. То есть, попытка такого формального представления ЗДО, которое дало бы тождественно истинную итоговую формулу. Причём, основываясь на минимуме аксиом.
Однако, во-вторых, в этой связи мне не понятен такой момент, касающийся дизъюнкции и конъюнкции прямых и обратных импликаций:
Точнее, с первой формулой всё ясно: (S → P) v (S ← P) ≡ (¬S v P v S v ¬P), и это, действительно, тождественно истинная формула. Но вот что (S → P) ∧ (S ← P) = 0 - это, на мой взгляд, неверно, в чём легко убедиться: (S → P) ∧ (S ← P) ≡ (S ∧ P) ∨ (¬S ∧ ¬P) ≡ (S ↔ P). В данном случае получается эквиваленция ("тогда и только тогда"), а не тождественно ложная формула. Здесь тождественно ложной является отрицание первой - т.е. ¬((S → P) v (S ← P)) ≡ ¬(S → P) ∧ ¬(S ← P), поэтому никак не (S → P) ∧ (S ← P). Или я чего-то не понял, и Вы нечто другое имели в виду?
Приветствую Юрий. Я совершенно неожиданно столкнулся с вербальным барьером. Даже моего, виртуозного я считаю, владения разговорным языком не всегда хватает, для того, чтобы адекватно отразить специфику проблематики.
Я строю такую логическую систему, которая будет опираться на одну единственную аксиому. Полный ряд 16 булевых функций. Их именно 16. Не больше и не меньше. Дальше эта замкнутая система опирается сама на себя, став самореферентной.
Это предельная строгость, которая накладывает ограничения.
Даже кванторы, которые мне нужны, я не могу использовать. В символьном обозначении булевых функций, кванторов нет. Поэтому я использую подсказку, которую в свое время вычитал у Зегета.
Зегет В. Элементарная логика. -- М.: 1985
Зегет предлагает использовать обозначение квантора в логике предикатов по желанию. Можно использовать, а можно и нет, чтоб не загромождать символьную запись. Дизъюнкция, которая оборачивается в импликацию либо репликацию всегда находится либо под квантором общности (∀х), либо под отрицанием квантора существования (¬∃х). Конъюнкция, наоборот, всегда находится либо под квантором существования (∃х), либо под отрицанием квантора общности (¬∀х).
Соответственно в предлагаемой системе введение v - означает одновременное введение ∀х, а введение ^ - означает одновременное введение ∃х.
Признаю. Система моих уравнений в таком виде
не полна.
Сущность формализованного ЗДО она не отражает. И Сергей Борчиков уже не раз мне про это говорил. Я графически показал место строгой дизъюнкции в системе, а в символьных записях это место не отразил. Ничего страшного, сейчас отражу.
Полная символизация формализованного ЗДО будет состоять из трех уравнений.
S - имя (частное), P - свойство (общее). Различие по порядку в символизации булевой функции. Имя никогда не может оказаться вторым по порядку, а свойство первым. Система собрана именно под такой порядок. Равно я уберу, а результат буду отражать в жирных скобках. Чтоб математика голову не путала.
Но порядок нолей и единиц в таблице истинности теперь тоже имеет значение. Поэтому дублирую сюда мой ответ Сергею.
Невероятно, но факт. Система реагирует на наполнение переменных. Это логические операции не с формами, а с содержанием. Форм всего 16 и они неизменны.
И давайте уже переселяться в гости к Сергею Борчикову. Мой неубиваемый мексиканец вновь активизировался, а санитары форума спят..
Мой последний комментарий здесь.
Кормин Михаил, 31 Январь, 2021 - 09:32, ссылка
Михаил, посмотрите, пожалуйста, сегодняшнее мое сообщение в личке.
Очень интересно, но пока еще не все понятно. )
Посылка включена в следствие.
Комментарии.
Несотворенность и самосотворенность.
В пределе, когда посылка равна следствию, получается самосотворенность и частный предельный случай цикличности.
Кстати, возможно это и есть причина склонности к цикличности в нашем мире.
*************************
Однако, тогда история должна накапливаться в настоящем.
Динамическая метафизика бытия
http://www.rodon.org/koltsov/dmb.htm
Там частично посылка включена в следствие.
Деревья качаются, потому что ветер дует (истинно)
Ветер дует, потому что деревья качаются (ложно)
*******************
Однако, если качать деревья, то на тебя вполне может подуть ветер, как от опахала.